最近，物理评论快报发表了物理系卢海舟教授课题组与合作者关于半导体-超导体纳米线中的Majorana振荡的最新理论进展。第一作者为博士后曹霑，通讯作者是卢海舟教授，合作者包括清华大学张浩教授，电子科技大学吕海峰教授，北京大学谢心澄院士。Majorana费米子是一种电中性费米子，它的反粒子是它本身。1937年意大利理论物理学家Ettore Majorana发表论文假想这种粒子存在，因此而命名。由于其遵循非阿贝尔统计，拓扑超导体中的Majorana束缚态可以用于拓扑量子计算，其研究目前受到微软等多家IT企业的资助。

       最近关于纳米线中Majorana振荡的实验和理论预言不符，Majorana束缚态的存在受到质疑。该理论进展通过提出非均匀自旋轨道耦合解释了最近的Majorana振荡实验。

       1. 什么是Majorana费米子

       大学量子力学的学习主要围绕求解Schrödinger方程展开

                                                                                          iℏ∂_t ψ=(-ℏ²/2m ∇²+V)ψ

       其中ψ是波函数，ℏ是约化Planck常量，i=√(-1)，m 是质量，V是势能，∂_t 表示对时间求导，iℏ∂_t是能量的算符，∇²表示对空间求二阶导数，来自动量算符-iℏ∇。这个方程在结合狭义相对论时候遇到了问题。在狭义相对论中，时间和空间被放到对等的位置，运动参考系中的时间和坐标一起遵循洛伦兹变换，即协变性。遗憾的是，Schrödinger方程的两边分别是时间的一阶导数和坐标的二阶导数，无法具有狭义相对论的协变性。

       为了解决这个问题，1928年英国理论物理学家Paul Dirac 提出了具有狭义相对论协变性的量子力学方程，用于表述自旋1/2的带电费米子，比如电子。Dirac方程预言了正电子，并很快被实验证实。Dirac方程可以在有电磁场和外势能的情况下自然给出薛定谔方程中的Zeeman效应和自旋轨道耦合等效应。最近，Dirac方程在各种拓扑物相的描述中更是发挥了重要的角色，其衍生的各种方程可以用于描述拓扑绝缘体，拓扑半金属，拓扑超导体。

        Dirac方程可以使用γ矩阵写成 (为写成协变形式，令 c=ℏ=1)

                                                                                               (iγ^μ ∂_μ-m)ψ=0

       其中 γ^μ 代表四个4×4 的矩阵，μ=0，1，2，3，其中 0代表时间，1，2，3代表三维空间， i∂₀ 表示对时间求导，是能量的算符，其它几个-i∂_μ 对三维坐标求导，是动量的算符。现在时间和空间都是一阶导数，因此Dirac方程可以满足狭义相对论协变性。Dirac方程中γ矩阵间互相间满足Clifford代数

                                              〖-(γ⁰)〗²=〖(γ¹)〗²=〖(γ²)〗²=〖(γ³)〗²=-1; γ^μ γ^ν=-γ^ν γ^μ 如果 μ≠ν.

       γ 矩阵的选择不是唯一的，每种选择称为一种表示, 比较有名的有Dirac，Weyl，Majorana三种表示 (图1)。Ettore Majorana于1937年提出了一种纯虚 γ 矩阵的表示，可以描述电中性自旋1/2粒子。这一方程的波函数只有实数解。从二次量子化的语言来说，复数波函数及其复共轭在二次量子化时候对应产生粒子的算符和消灭粒子的算符。Majorana的纯实数波函数的复共轭就是自己，因此描述的粒子为自身的反粒子, 即Majorana费米子的产生与湮没 (或者说产生其反粒子) 是一样的。

寻找Majorana费米子断断续续进行了大半个世纪，候选者包括中微子，超对称理论中光子的超对称自旋1/2费米子伙伴，天体暗物质中的弱相互作用有质量粒子等。本文只讲最近的在凝聚态物理学里的进展。

 
图1：从左到右依次为Erwin Schrödinger，Paul Dirac，伦敦西敏寺Dirac纪念石上镌刻着Dirac方程, Hermann Weyl, Ettore Majorana。Dirac方程有Dirac, Weyl, Majorana表示。

       2. Majorana束缚态与拓扑量子计算

      Majorana费米子的研究的重要性来自两方面，其一是它可能是一种基本粒子，其二是在凝聚态系统中可以找到与Majorana费米子相关的准粒子Majorana束缚态，可能用于拓扑量子计算。这种量子计算被称为拓扑量子计算，这个名称有两层含义。第一，Majorana束缚态通常是一个拓扑超导体的边界态或半整数磁场涡旋束缚态，其存在是拓扑超导体全局的拓扑性质决定的；其次，Majorana费米子遵循非阿贝尔统计 (non-Abelian statistics)，操作Majorana费米子直接改变系统基态，这也是拓扑非平庸的。在Majorana的表象里，电子被理解成了2个Majorana费米子，如果把它们放到空间上不同的点上，就可以利用单个Majorana费米子的非阿贝尔统计性质定义量子位 (Qubit)。最小的量子位需要两对Majorana费米子对，即四个Majorana费米子。同一对内的两个Majorana费米子交换只会改变波函数相位。与此对比，当来自不同对的两个Majorana费米子进行交换 (被称作braiding) 的时候，这四个Majorana费米子构成的多体系统的基态会被改变(图2)。不同的基态即可用于定义量子比特的不同状态。特别是，要消灭Majorana费米子必须改变系统全局的拓扑性质，两个成对的费米子原则上可以距离很远产生联系，称为非定域性(Nonlocality)，单个Majorana费米子不能被局域地消灭，这样的量子比特可以抵抗外界扰动，所以这种拓扑量子计算具有容错性。这些是利用Majorana束缚态进行量子计算的优点。
 

      图2: (1) Majorana费米子定义的量子位需要至少两个Majorana费米子对，虚线代表配对；(2)来自不同对的两个Majorana费米子进行交换 (braiding)，四个Majorana费米子构成的多体系统的基态会被改变，从而定义量子位。

       3. 凝聚态物理中的Majorana束缚态

       目前在凝聚态系统实现的Majorana费米子的主流方案是基于拓扑p波超导体。在二维p波超导体中，Majorana束缚态可以存在于磁场造成的半整数涡旋处。在一维p波超导体中，Majorana束缚态可以处于拓扑非平庸和平庸的界面。为什么是超导体？因为Majorana既然是自己的反粒子，消灭一个和产生一个是一样的，不满足粒子数守恒，超导体或者超流体符合这个要求。另外，拓扑超导体的拓扑边界态或束缚态的能量上处于超导能隙的中间。超导体自带电子-空穴对称性，超导能隙内的拓扑边界态或束缚态只能携带零能量，满足粒子是反粒子的条件。为什么是p波超导体？因为描述超导体的BdG方程在配对为p波的时候等价于有拓扑描述的有质量Dirac模型, 可以自然的定义一个类似拓扑陈数的拓扑数，通过拓扑体系普适的体态-边界对应性可知，一定存在拓扑边界态或缺陷束缚态。一维p波超导有拓扑边界态也是类似的道理。此外，p波超导体的方案其实是无自旋的，和Ettore Majorana定义的自旋1/2Majorana费米子不同。没有自旋的费米子要求超导配对是奇宇称的。p波是满足奇宇称超导配对的最简单形式。由于电子遵循费米统计，这种配对要求参加配对的两个电子的自旋同向极化 (即Triplet三重态)。由于自旋完全朝着一个方向极化，就等于没有自旋了。比较著名的p波超导体模型包括Kitaev一维无自旋链p波超导体，付亮-Kane的拓扑绝缘体-s波超导界面的二维模型等。这些模型中的“Majorana费米子”都不带自旋，只是承袭了Majorana 费米子零能和非阿贝尔统计的性质，被称作 Majorana zero mode (零能模)更合适。

       4. 半导体-超导体纳米线方案

       Majorana研究从理论到实验的突破来自基于半导体-超导体纳米线的方案，算是Kitaev一维无自旋链p波超导体的一种实现 (图3)。美国马里兰大学和以色列的两个研究小组相隔不到两星期分别在arXiv 预印本网站张贴了类似的方案。该方案需要三个配料: (1) 一根自旋轨道耦合很强且g因子很大的纳米线; (2) 在其上附着一个s波超导体; (3) 垂直于自旋轨道耦合方向的磁场。一对零维的Majorana束缚态会分别占据这种纳米线系统的两端。自旋轨道耦合的作用是配合s波超导配对产生p波超导配对。g因子的作用有两个，一是利用Zeeman劈裂破缺自旋简并，制造无自旋(自旋极化)的条件，二是需要Zeeman劈裂足够大引发p波超导体从拓扑平庸到拓扑超导的相变，Zeeman能Vz必须大于 √(μ²+Δ² )，其中μ 是化学势，Δ是s波超导配对大小。

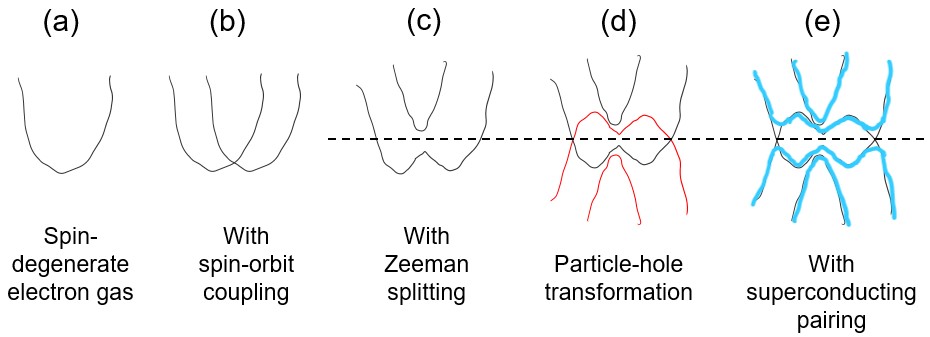
图3: 利用半导体-超导体纳米线实现Kitaev 一维无自旋链p波超导体 [Kitaev01] 的方案的能谱示意图。横轴是动量，纵轴是能量。(a) 从一个电子气出发，一维或二维均可; (b) 自旋轨道耦合破除自旋简并; (c) 加入Zeeman能，使得费米能 (虚线) 只切过一个能带，实现无自旋(自旋极化)的描述; (d) 粒子-空穴变换，为加入超导能隙做准备。(e) 加入超导配对，打开超导能隙。这个例子中Zeeman能已经足够大，所以已经是p波超导体。

       2012年4月中旬，一个星期内两个实验组在arXiv网站上发布了支持Majorana束缚态的实验结果，包括荷兰Delft理工大学的Kouwenhoven实验组使用半导体InSb-超导体NbTiN纳米线和北京大学的徐洪起教授实验组使用Nb-InSb纳米线约瑟夫森节。5月底，以色列威兹曼研究所使用InAs-Al也观察到了类似的实验结果。支持Majorana 束缚态的实验证据是微分电导dI/dV 在磁场超过超导拓扑相变临界磁场后出现了一个零偏压电导峰，其中I是电流，V是偏压 (图4 a)。这几个实验出来后，关于测量到的信号是不是来自Majorana束缚态出现了各种争论，比如无序也可以给出零偏压电导峰，非常热闹。香港科技大学罗锦团, 吴大琪和MIT的李雅达理论预测Majorana零能模将给出2e2/h的量子化微分电导峰值，被最近荷兰Delft理工大学Kouwenhoven组实验验证，文章第一作者张浩最近加入了清华大学，开始组建独立的研究小组。除此之外，还有更多的系统可以实现这种p波拓扑超导体。比如普林斯顿大学Yazdani团队使用低温扫描隧道显微镜发现在超导铅薄膜表面的一条铁原子链的两端会出现零能电导峰。上海交通大学贾金锋团队先是2015年在Bi2Te3/NbSe2 薄膜中报道了STM探测到的具有零能的漩涡态, 继而在2016年与浙江大学张富春，南京大学李绍春合作证明这种零能态的安德烈夫反射自旋选择性，为Majorana 束缚态提供了另外一种判据。2015年，潘庶亨团队报道了在Fe(Te,Se)超导体中，利用STM在单个铁杂质的中心可以观察到超导能隙内的零能束缚态。这个束缚态可以在高达8T的磁场中存在，并且不受临近的杂质的影响，符合Majorana束缚态的性质。
2018年，物理所丁洪研究员团队先是和东京大学Shik Shin 教授，张鹏博士等合作报道FeTe0.55Se0.45表面存在二维无质量Dirac拓扑表面态和s波超导，满足了付亮-Kane 二维p波拓扑超导的元素，继而与高鸿钧院士团队合作报道其表面的磁场涡旋处存在超导能隙内Majorana束缚态导致的电导峰。Boston college的汪自强教授和蒋坤博士，香港科技大学戴希教授理论认为FeTeSe超导中存在的是一种无需磁场只需磁性杂质的反常涡旋，这样可以空间定位Majorana束缚态，有利于对Majorana束缚态实现Braiding操作。

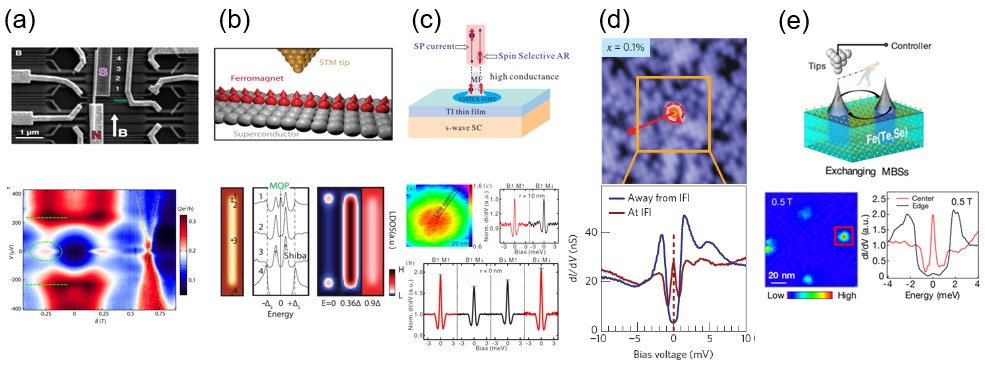
图4: 几种目前观察到Majorana束缚态的实验系统。(a) 半导体-超导体纳米线; (b) 超导铅薄膜上的铁原子链; (c) s波超导体上的拓扑绝缘体薄膜; (d-e) Fe(Te,Se)表面。

       5. Majorana束缚态的能量劈裂和Majorana振荡

       有一个原因导致Majorana 零模这个名字不太合适。Majorana束缚态必须成对出现。在有限大小系统，成对的两个Majorana束缚态会相互耦合，造成能量发生劈裂！Mojorana费米子的零能性质实际上是没有的。

理论发现，Majorana束缚态能量的劈裂会随着磁场振荡，振幅随着磁场越来越大 (图5)，这曾经被认为是Majorana的另一个smoking-gun 证据。

图5: 早期理论预言的Majorana束缚态的劈裂能振荡，振荡幅度随磁场的Zeeman能的增大而增强。

       但是，与这个预言相反，最近的实验都观测到Majorana振荡的振幅随着磁场增大而衰减(图6 b-c)。过去几年中，各种理论被提出去解释这个衰减的振荡，但是都不太成功。实验探测到的是否真的Majorana 束缚态？这会不会破坏欣欣向荣的Majorana拓扑量子计算研究的基石？

       6. 衰减Majorna振荡的理论解释: 非均匀自旋轨道耦合

       这个问题最终被最新的理论工作解决。最新的理论发现，实验以及以前的理论都忽略了一个的因素：实验的纳米线中的自旋轨道耦合不是均匀的。在纳米线结构中电极和超导体的电场以及屏蔽效应都会调制自旋轨道耦合的大小，造成空间不均匀。最简单的模型可以假设纳米线分成自旋耦合大小不同的两段。这个假设立刻能给出衰减的Majorana振荡。其衰减机制是：随着磁场的增大，两段纳米线之间的耦合增强导致二者能谱之间的相互排斥增强，使得能量较低的能谱在振荡的同时变得更低。通过更仔细的参数调节，在不同长度纳米线中观测到的各种形状的衰减都可以被拟合，更加确定了不均匀自旋轨道耦合在纳米线中的存在。此外，这个理论发现，存在不均匀自旋轨道耦合的时候，纳米线中的另一种拓扑束缚态Andreev束缚态也会产生衰减振荡。最新的实验也支持了非均匀自旋轨道耦合是纳米线中不可忽视的因素。

 
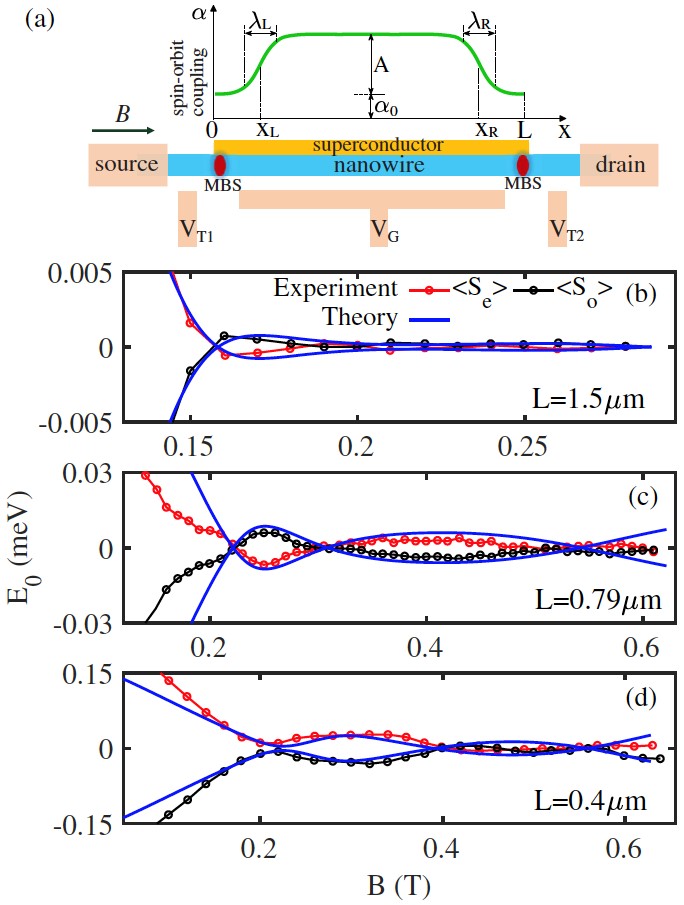
图6：最新的理论进展利用非均匀自旋轨道耦合 (a图绿线) 系统地解释了半导体-超导体纳米线系统中的衰减Majorana振荡。b-d图蓝实线为理论计算结果，红黑点线为实验数据。

       7. 展望

       过去十年，Majorana束缚态和相关的拓扑量子计算的研究不断向前，虽然我们已经知道凝聚态物理中的Majorana束缚态和粒子物理中的Majorana费米子不同，既没有1/2自旋也不是绝对零能。未来更重要的是利用Majorana束缚态的非阿贝尔统计和braiding操作实现可容错的拓扑量子计算。

       文章链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.147701