Optical trapping and binding were discovered in 1969 and 1989, respectively. Since then, they have attracted broad and continuous interest across many disciplines, which includes, but is not limited to, biology, colloidal science, and essentially anywhere that small particles manipulation plays a role. Its pioneer, Arthur Ashkin, was awarded the Nobel Prize in 2018.

Non-Hermitian physics is also a burgeoning area that has attracted much interest recently. This work aims to show that these two seemingly unrelated topics are connected. By applying the non-Hermitian theory to study optical trapping and binding, we see the emergence of surprising physics and a deeper understanding from this decades-old field.

Associate Professor Jack Ng’s (Zihui Wu) group from the Department of Physics at the Southern University of Science and Technology (SUSTech) has reported their latest work on the consequence of non-Hermiticity in optical trapping and binding. Their work, entitled “Non-Hermitian physics for optical manipulation uncovers inherent instability of large clusters,” was published in the high-impact academic journal Nature Communications.

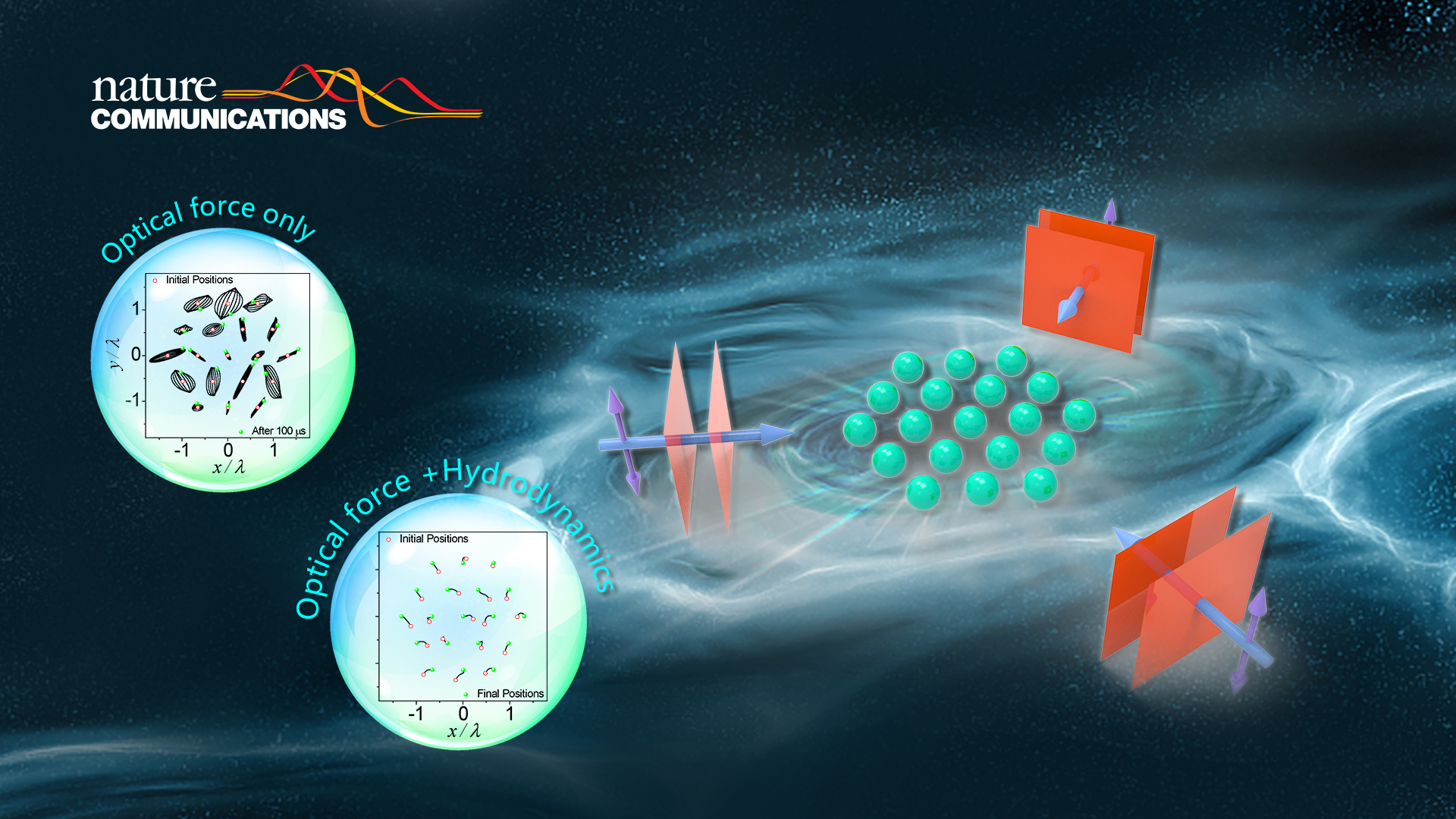
Optical binding is the coupling of particles via light scattering that alters the optical force. Its well-accepted theory claims particles will form an energetically favorable entity called “optical molecule” or even “macroscopic optical matter”, just like ordinary materials bound by electrons. However, unlike the Hermitian electronic binding, the non-conservative optical binding is non-Hermitian, where the conventional theory (energy mini-max principle) does not apply. From here, the researchers found surprising physics.

Exceptional points, the singular point of the vibration spectrum, are found in optical binding. It signifies a stable-unstable symmetry-breaking phase transition, where the vibration frequencies turn complex, allowing light to “pump in” energy and “melt” the structure. More importantly, the instability threshold will always be reached for a sufficiently large cluster because the vibration spectrum will approach degeneracy. This allows the tiniest non-Hermitian coupling to drive the system through the exceptional points, independent of details. In short, optical force alone cannot bind a large cluster.

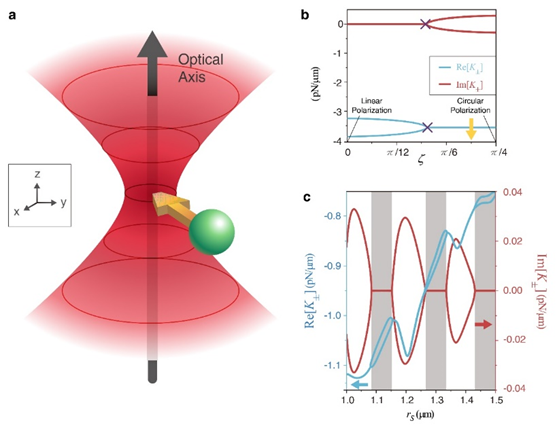
Figure 1. Exceptional point in optical trapping of a single particle. (a) Schematic of the optical trapping of a dielectric particle. (b) The purple crosses mark the exceptional point, with the trapping stable on the left and unstable on the right side of the exceptional point. (c) The stability also depends on the particle size.

Nevertheless, the researchers were initially challenged by others, who claimed that the theory contradicts existing experiments, where stable clusters are observed. The issue was finally resolved by recognizing that the stability observed could not be solely achieved by optical binding as claimed by many, but auxiliary damping is necessary. The old term optical binding is better termed “Opto-hydrodynamic binding” for large clusters. In fact, by large clusters, they mean clusters with ~10 particles or more.

Here, non-Hermiticity is the key, whose physical origin is the incoming illumination and the radiative loss. Particles do not always go to the energetically favorable position. When two vibration frequencies are nearly degenerate, the non-conservative force will serve as a pump that excites and destabilizes the cluster.

On the one hand, their theory replaces the old optical trapping and binding theory, and on the other hand, expands the realm of non-Hermitian physics.

Figure 2. Prevalence of complex unstable modes with increasing particles. (a) The percentage of complex unstable modes (CMs) increases with particle number for all considered geometries shown in the panel. (b-g) Indicating that large clusters are intrinsically unstable.

The theory and mathematical framework that Prof. Ng’s team has developed can be applied to any open system with positional non-conservative force, including acoustic forces and other systems bound by radiation.

Xiao Li, a visiting scholar in Prof. Jack Ng’s (Zihui Wu) group, is the first author of this paper. Jack Ng (Zihui Wu) is the corresponding author. Significant contributions were also made by Assistant Prof. Yineng Liu from Xiamen University, Prof. Zhifang Lin from Fudan University, and Prof. C. T. Chan from the Hong Kong University of Science and Technology (HKUST).

This work was supported by the National Natural Science Foundation of China (NSFC), the Shenzhen Natural Science Fund, the Hong Kong Research Grants Council (HKRGC), and the Croucher Foundation.

Paper link: https://www.nature.com/articles/s41467-021-26732-8