Researchers make breakthrough in magnetic geometry-induced quantum geometry and nonlinear transport
2025-06-06SUSTech hosts IOP Forum with President of Institute of Physics Sir Keith Burnett
2025-03-26Researchers discover unusual thermal conductivity in high-symmetry single crystals
2025-03-26New efficient method detects quantum temporal correlations
2025-03-26Researchers explore unconventional magnons predicted by spin space groups
2025-03-25On September 1st and 8th, Physical Review Letters (PRL) accepted two works by Associate Professor Hai-Zhou Lu’s group in Department of Physics and Institute for Quantum Science and Engineering. One title is “3D quantum Hall effect of Fermi arcs in topological semimetals”,the other is “Negative magnetoresistance without chiral anomaly in topological insulators”.
In the first one, they predicted a new quantum Hall effect that can occur in 3D. In a strong magnetic field, a moving charge feels a Lorentz force that is normal to both its velocity and the magnetic field, giving rise to a Hall resistance. In 1979, von Klitzing discovered that the Hall resistance of a 2D electron gas can be quantized into a series of plateaus in terms of (h/e2)/n, where e is the elementary charge, h is Planck’s constant, n is an integer known as “Chern numnber” (named after mathematician Shiing-Shen Chern). This quantized Hall effect opened the door towards a large field of research on topological phases of matter, leading to three Nobel Prizes in physics (1985 von Klitzing, 1998 Tsui, Stormer, Laughlin; 2006 Thouless, Haldane, Kosterlitz). The quantum Hall effect is because the cyclotron motion of a 2D electron gas quantizes its energy spectrum into Landau levels under strong magnetic fields. The Landau levels can form 1D dissipationless conducting channels at the edges of a sample, each contributes a Hall conductance of e2/h,resulting the quantized Hall resistance (Figure 1). In 3D, the Hall resistance also depends on thickness, so usually there is no quantized Hall effect.
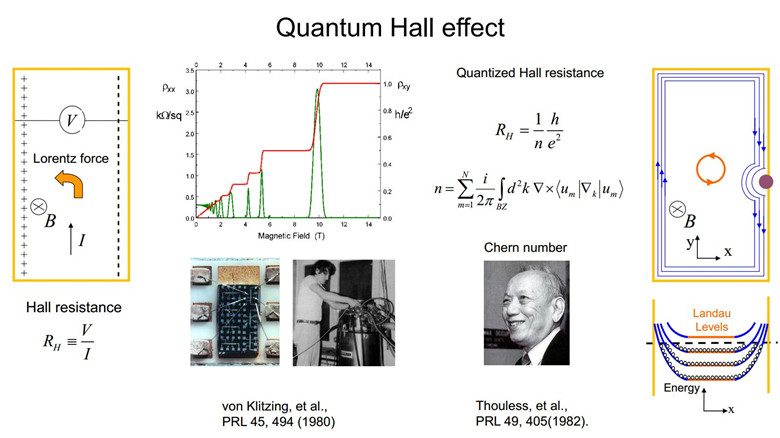
Figure 1. The quantum Hall effect.
In their new work, Hai-Zhou Lu and his colleagues revealed that, a 3D quantum Hall effect can be realized in a topological semimetal (Figure 2). Topological semimetal is a new family member of topological phases of matter. They have topologically protected surface states, dubbed the Fermi arcs. Because of topological constraint, the Fermi arc at a single surface can occupy only a certain area in momentum space, so it cannot support a complete cyclotron motion and quantum Hall effect. However, they found that, electrons can perform half of a cyclotron at one surface, then tunnel to the opposite surface via the Weyl nodes, and complete the other half of the cyclotron motion. The Weyl nodes are points at which the conduction and valence bands touch in a topological semimetal. According to the uncertainty principle of quantum mechanics, the Weyl nodes are singularities in momentum and energy, so they are infinite in space and time. In principle, they can connect two Fermi arcs infinitely far away from each other. This mechanism is similar to the wormhole effect of general theory of relativity, i.e., two low-dimensional space-time can be connected by a higher-dimensional singularity. Signatures of this “wormhole” tunneling assisted 3D quantum Hall effect probably have been probed by recent experiments (Uchida et al., APS March Meeting A44.00005 (2017); Zhang et al., arXiv:1612.05873v2, Nature Commun. to appear).
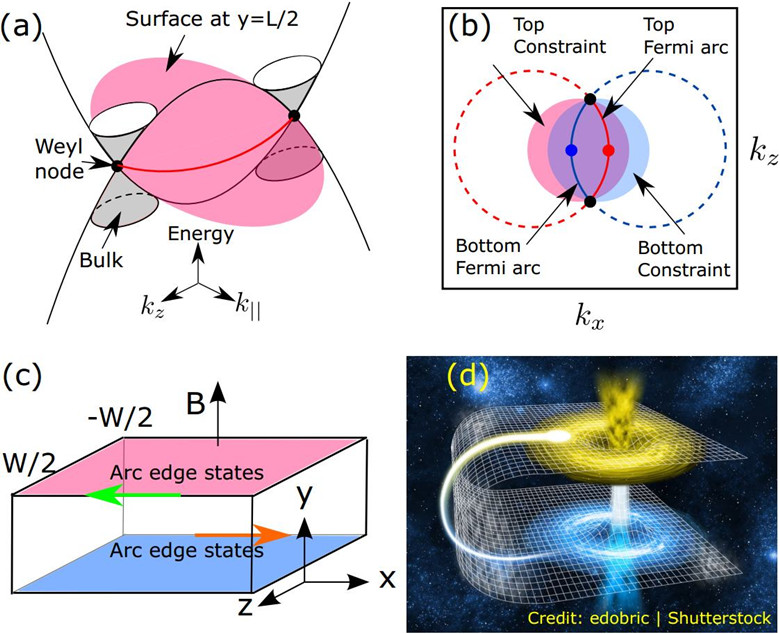
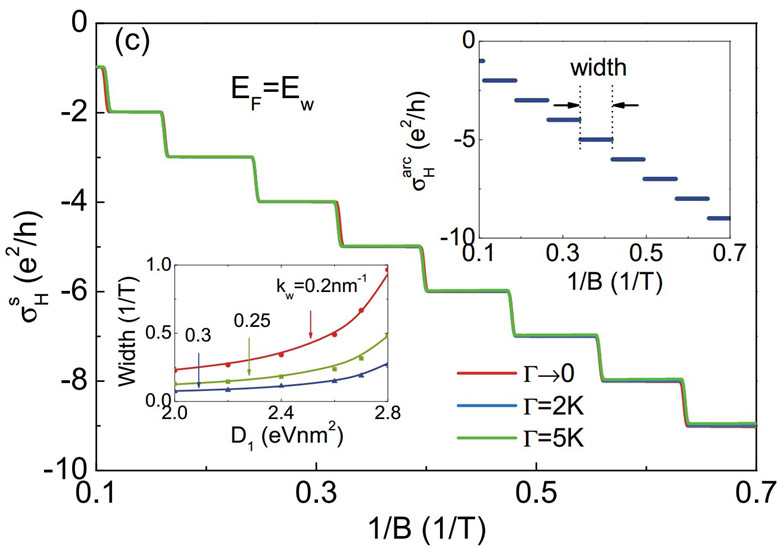
Figure 2. 3D quantum Hall effect of Fermi arcs in a topological semimetal and the “wormhole” effect.
In the other work, they gave a possible explanation to some confusing experiments on topological insulators. A magnetic field usually prevents electrons from moving forward, so usually in non-ferromagnetic materials the resistance increases with increasing magnetic field, giving rise to a positive magnetoresistance. It is rare in nature to observe a negative magnetoresistance (except the weak localization effect), i.e., the resistance drops with increasing magnetic field, in particular at higher temperatures. Since 2010, a negative magnetoresistance has been observed in topological insulators and topological semimetals. Since 2013, the negative magnetoresistance in topological semimetals has been interpreted as a result of the chiral anomaly, that is, the quantization breaks the chiral symmetry, a concept from high-energy physics. However, in topological insulators, there is no well-defined chirality, not to mention the chiral anomaly. To look for the answer to this confusion, they tried to start from a more fundamental formulism, the Sundaram-Niu equations of motion. According to the equations, an anomalous current can arise as long as there is a nontrivial distribution of the Berry curvature (a “magnetic field” in momentum space, named after British theoretical physicist Michael Berry, who got Ig Nobel Prize in 2000 with A. Geim, who has a real Nobel Prize as co-discoverer of graphene). The anomalous current increases with increasing magnetic field, in other words, it reduces the resistance and leads to a negative magnetoresistance. To verify their theory, Hai-Zhou Lu and his colleagues have performed a huge amount of numerical simulations using the high-performance computing facilities in the Department of Physics at SUSTech. Eventually, they arrived at a good agreement between the experiments and their theoretical results. This is by far the best understanding to the novel negative magnetoresistance in topological insulators (Figure 3).

Figure 3. (a) The Berry curvature in a topological insulator. (b)-(d) The comparison of the negative magnetoresistance in the experiments and theory.
These works were supported by MOST, NNSFC, Guangdong Province, Shenzhen Key Lab, and SUSTech.
The papers can be found at
C. M. Wang, H. P. Sun, H. Z. Lu*, and X. C. Xie, arXiv: 1705.07403, PRL (2017).
X. Dai, Z. Z. Du, and H. Z. Lu*, arXiv:1705.02724, PRL (2017).
https://journals.aps.org/prl/accepted/4e078Y2aR041f562a25360b1197b67a9043020ac0
https://journals.aps.org/prl/accepted/b5071Yd9Rcb1916d12262100c42e6664af2ed6540