In condensed matter physics, quasiparticles are quantized manifestations of collective excitations and are used to describe the low-energy dynamics of systems in a particle-like manner. For instance, phonons represent elementary excitations of periodic lattice vibrations in crystals, whose quantum characteristics determine thermal conductivity and lattice vibration band structure in solids.

Magnons, the quantized excitations of spin waves—propagating disturbances of magnetic order in magnetic materials—reflect the low-energy fluctuation properties of magnetically ordered systems. These quasiparticles possess particle-like attributes, such as energy and momentum, while they essentially correspond to the “emergent phenomena” from the cooperative interactions of numerous microscopic particles. Their existence reveals simplified descriptions of complex many-body systems and serves as crucial theoretical tools for understanding macroscopic material properties and phase transition mechanisms.

The transport of magnon is independent of electron charge, thereby avoiding Joule heating and exhibiting low dissipation, with transmission distances reaching millimeter scales. This makes magnons ideal carriers for information transmission and processing. However, controlling the transport direction of magnon remains challenging, prompting researchers to investigate topological magnon systems combining low dissipation with topologically protected directional transport.

Recent breakthroughs in topological quantum chemistry and symmetry indicator theory have significantly accelerated the topological diagnosis and high-throughput computation of quantum materials based on crystal symmetry and topological band theory. This progress has expanded the search for topological states from fermionic electron systems to bosonic systems like phonons and magnons.

Professor Qihang Liu’s research group from the Department of Physics at the Southern University of Science and Technology (SUSTech) has recently made progress in the theory of collinear spin groups and the complete classification of unconventional magnons in collinear magnets.

Their work, entitled “Unconventional magnons in collinear magnets dictated by spin space groups”, has been published in the journal Nature.

Traditional topological band theory relies on magnetic space group symmetries. However, extending topological quantum chemistry diagnostics from electrons to magnons faces a major challenge: the fundamental symmetry description of magnetic materials. Conventional magnetic space group theory has long struggled to explain complex magnon behaviors observed experimentally, such as nodal points with extra degeneracy in magnon bands revealed by inelastic neutron scattering. This limitation stems from the inherent incompleteness of magnetic space groups in describing the full geometric symmetries of magnetic materials, particularly failing to fully capture exchange interaction-dominated properties in magnetic systems.

In collinear magnets, magnon dynamics are primarily governed by isotropic Heisenberg exchange interactions, while spin-orbit coupling effects, such as Dzyaloshinskii-Moriya interactions, are often negligible. Consequently, magnon Hamiltonians encompass not only completely coupled operations of magnetic space groups but also additional partially decoupled symmetry operations between spin space and lattice space. Together, these symmetries form a larger group known as the spin space group. While crystal and magnetic group theories were fully established decades ago and standardized in textbooks, research on spin groups—particularly fundamental theories of spin space groups—remains in its infancy globally.

Since 2021, Professor Qihang Liu’s team has pioneered a new theoretical framework for spin groups, achieving significant results, including classification and representation theories of spin point groups and spin space groups (Phys. Rev. X 12, 021016 (2022); Phys. Rev. X 14, 031038 (2024)). Their latest work focuses on collinear spin space groups describing collinear magnets, forming the theoretical basis for the emerging research field of “altermagnetism”. The 1,421 collinear spin space groups exhibit group structures expressible as direct products of the nontrivial spin space and spin-only groups. The former corresponds isomorphically to type I, III, and IV magnetic space groups, while the latter constitutes a Lie group containing SO(2) rotations and spin mirrors.

The existence of a spin-only group fundamentally differentiates the representation theories of collinear spin space groups from those of conventional magnetic space groups. The team systematically developed collinear spin space group theory, including general positions, Wyckoff positions and site spin groups, spin Brillouin zones and wavevector little co-groups, band representations, and topological quantum chemistry theory. These results have been compiled in an open-access database integrated into their self-developed online interactive platform, FINDSPINGROUP (see link below).

Based on the structures of collinear spin space groups and their correspondence with magnetic space groups, collinear magnets can be classified into four categories. The first category consists of 230 type I groups describing single magnetic sublattices, corresponding to collinear ferromagnets and collinear ferrimagnets (including compensated ferrimagnets) with multiple symmetry-unrelated magnetic sublattices. The second category includes 674 groups describing two magnetic sublattices in primitive Bravais lattices. Based on whether the symmetries connecting opposition-spin sublattices contain spatial inversion P, these are further divided into another two categories, i.e., 252 type II and 422 type III collinear spin space groups, which correspond to PT collinear antiferromagnets (the combination of spatial inversion P and time reversal T) and altermagnets, respectively. The fourth category comprises 517 type IV groups, which describe black-and-white Bravais lattices and correspond to Uτ collinear antiferromagnets (the combination of the spin-reversal U and the fractional lattice translation τ).

Figure 1 illustrates the distribution of these five types of collinear magnets within the MAGNDATA magnetic materials database, along with representative examples. Notably, while both PT and Uτ collinear antiferromagnets exhibit electronic spin degeneracy or magnon chiral degeneracy, their topological node characteristics differ fundamentally. When the topological charge is allowed in one spin channel, PT collinear antiferromagnets show opposite topological charges between two opposite spin channels, whereas Uτ collinear antiferromagnets maintain identical charges.

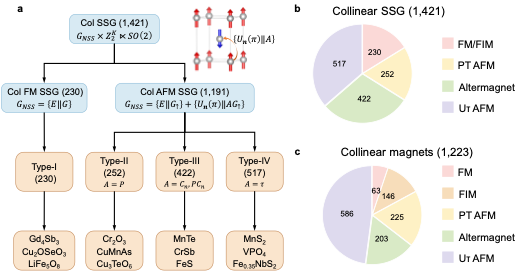
Figure 1. Classification of collinear spin space groups and collinear magnets

The representation theory of spin space groups explains non-relativistic band degeneracies and splittings in magnetic materials beyond the magnetic space group framework. Building on this, the team established a magnon nodal topology classification scheme and identified novel quasiparticle states beyond magnetic space group descriptions. These include magnons with non-zero topological charge C, such as C=4 octuple/sextuple nodes and C=8 Dirac magnons. Additionally, the identified zero-charge magnons, including duodecuple, octuple, sextuple, and triple nodes. Other newly classified states include octuple nodal line magnons, quadruple nodal plane magnons, and momentum-dependent chiral splitting magnons.

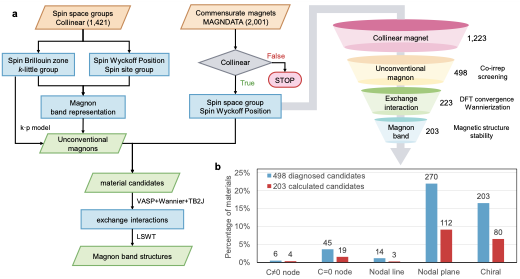
Figure 2. Workflow for unconventional magnon database construction

Through high-throughput topological diagnosis and magnon band calculations using the MAGNDATA database (Figure 2), the researchers identified 1,223 collinear magnets from over 2,000 magnetic materials, with 498 candidates hosting at least one unconventional magnon type. First-principles and linear spin wave theory calculations ultimately established a magnetic exchange parameter database containing 223 materials, confirming 203 materials with unconventional magnons.

For instance, altermagnet FeS was found to exhibit octuple degeneracy and chiral splitting, guiding experimental observation of nonreciprocal magnon transport. Meanwhile, the Uτ antiferromagnet Fe₀.₃₅NbS₂ hosts coexisting C-4 octuple nodes and a quadruple nodal plane network. Systematic calculations show the spin-orbit coupling-induced magnetic exchange interactions remain below 10% of Heisenberg exchange in more than 80% of candidates, validating the theory’s universality in 3d/4d and half-filled 4f magnets.

While single-valued band representations for bosons (e.g., magnon) and double-valued band representations for fermions (e.g., electron) differ fundamentally in conventional symmetry frameworks, the spin SO(2) symmetry renders their single- and double-valued band representation forms identical dimension, differing only in the matrix representation due to the spin angular momentum 1 (for magnons) vs. ½ (for electrons). This enables direct generalization of magnon band representations in collinear magnets to electronic band structure, explaining identical momentum-dependent electronic spin and magnonic chirality splitting in altermagnets.

The spin group concept, first proposed by Brinkman et al. in 1966 to explain extra magnon band degeneracies, remained unresolved for half a century. Through the comprehensive development of spin space group theory, Professor Liu’s team has systematically predicted magnon band degeneracies. Their work opens new avenues for exploring topological magnon states and designing novel materials.

The authors of this paper are all from Qihang Liu’s research group from the Department of Physics at SUSTech. The first author is postdoctoral researcher Xiaobing Chen (currently an Associate Researcher at the Quantum Science Center of Guangdong–Hong Kong–Macao Greater Bay Area). Other collaborators include Ph.D. Yuntian Liu (currently a postdoctoral researcher at the University at Buffalo, State University of New York), Ph.D. student Pengfei Liu, master’s student Yutong Yu, master’s graduate Jun Ren, Ph.D. Jiayu Li (currently a postdoctoral researcher at the University of Hong Kong), and postdoctoral researcher Ao Zhang. Professor Qihang Liu is the corresponding author, and SUSTech is the primary affiliation of the paper.

Paper link: https://www.nature.com/articles/s41586-025-08715-7

FINDSPINGROUP link: https://www.findspingroup.com/database/