Researchers make breakthrough in magnetic geometry-induced quantum geometry and nonlinear transport
2025-06-06SUSTech hosts IOP Forum with President of Institute of Physics Sir Keith Burnett
2025-03-26Researchers discover unusual thermal conductivity in high-symmetry single crystals
2025-03-26New efficient method detects quantum temporal correlations
2025-03-26Researchers explore unconventional magnons predicted by spin space groups
2025-03-25Antiferromagnetic materials, characterized by opposing magnetic alignments of neighboring spins, exhibit unique electronic structures that significantly differ from their ferromagnetic counterparts. Conventional antiferromagnets exhibit no splitting of electronic spin in their energy bands because of the symmetry of magnetic elements. In this work, however, researchers uncover giant spin splitting in the bands of an “unconventional antiferromagnet”, a kind of novel material that enables spin polarization due to the exotic interplay between the crystalline symmetry and the magnetic order.
Unraveling this phenomenon not only enhances our fundamental understanding of magnetic materials but also paves the way for technological advancements in areas such as spintronics and magnetic storage media. Moreover, delving deeper into the spin splitting of energy bands opens avenues for designing materials with tailored magnetic and electronic properties, expanding the toolkit for scientists seeking to optimize performance in spintronic devices.

A research team led by Associate Professor Chang Liu and Professor Qihang Liu from the Department of Physics and the Shenzhen Institute for Quantum Science and Engineering (SIQSE) at the Southern University of Science and Technology (SUSTech), in collaboration with Researcher Shan Qiao from the Shanghai Institute of Microsystem and Information Technology of the Chinese Academy of Sciences, have made progress in the research of the electronic structure of antiferromagnetic materials. They directly observed the spin splitting of energy bands in antiferromagnetic materials for the first time.
Their related results, entitled “Observation of plaid-like spin splitting in a noncoplanar antiferromagnet”, were published in the journal Nature.
The magnetism of solids originates from the ordered arrangement of magnetic moments of the atoms that make up the lattice. An atom with magnetic moments can be seen as a tiny magnet with north and south poles. Ferromagnets have macroscopic magnetism because the magnetic moments of all magnetic atoms are arranged in the same direction (Figure 1a). Antiferromagnets do not have macroscopic magnetism because the magnetic moments are arranged in opposite directions, which can be “up-down-up-down” (Figure 1b), “up-up-down-down” or the like, resulting in zero net magnetic moments.
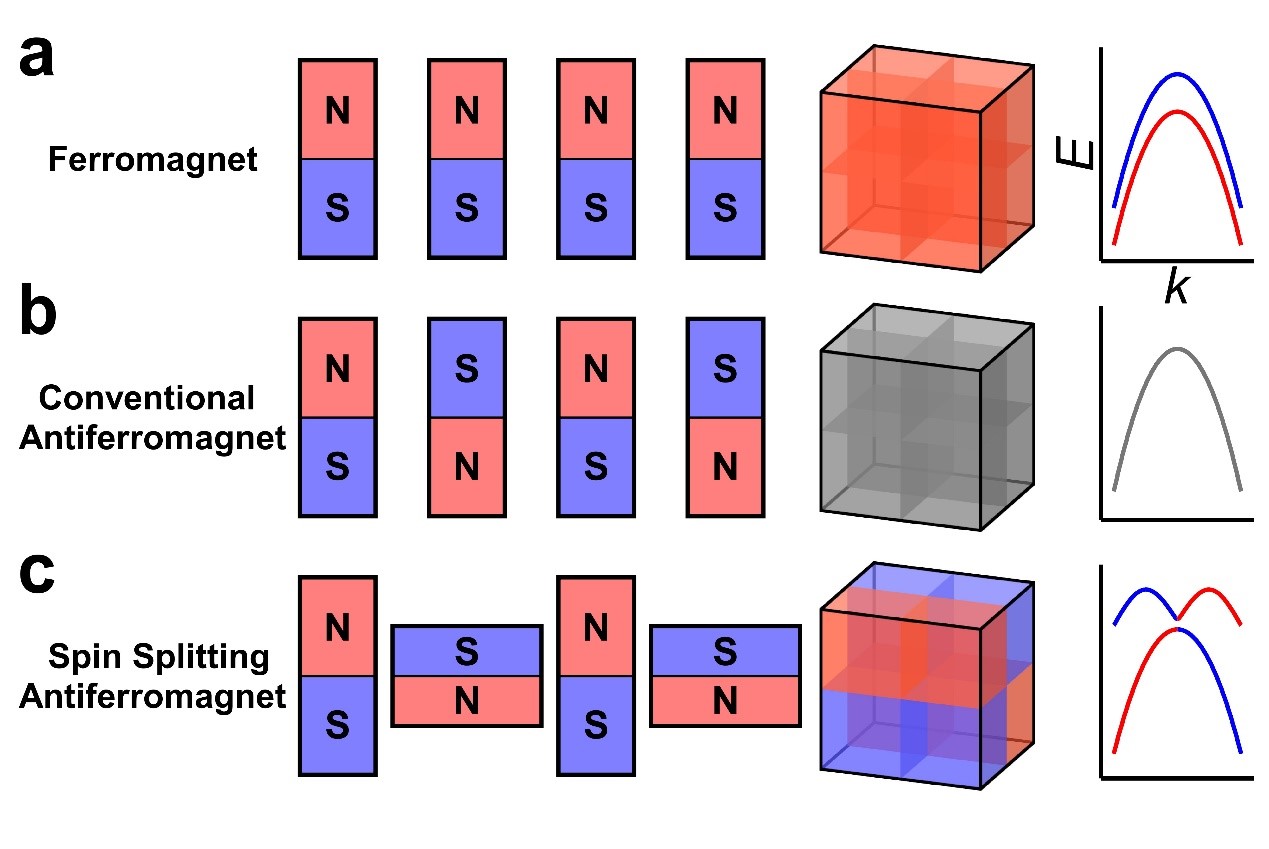
Figure 1. Spin-polarized charge density of ferromagnets, conventional antiferromagnets, and unconventional antiferromagnets with spin splitting, as well as the distribution of spin polarization in the three-dimensional Brillouin zone and a schematic diagram of spin-resolved energy bands.
If an electron travels through the ferromagnet shown in Figure 1a, the probability of its magnetic moment (electron has spin, therefore also has magnetic moment) facing downwards will be greater than the probability of its magnetic moment facing upwards because the N pole of the atomic magnetic moment and the S pole of the electron magnetic moment are attracted to each other. This situation is known as “spin splitting of the energy band”, where the energy of the system is lower when the electron is in the spin-down energy band than when it is in the spin-up energy band, and low energy states are more prone to occur. The red energy band in the right panel of Figure 1a contains electrons with downward magnetic moments, which is located at a lower energy axis position. The spin polarization current caused by spin splitting in ferromagnets directly leads to the anomalous Hall effect and the magneto-optical effect, triggering the frontier discipline of spintronics.
At present, most spintronic devices use ferromagnets as manipulators for spin flow, utilizing the spin of electrons as carriers to generate, store, and read/write information by detecting and manipulating the spin state. This discipline has now developed into a hot topic in physics and materials science research, bringing about innovations such as high-capacity magnetic random access memory that have had a profound impact on humanity.
If an electron travels through the conventional antiferromagnet shown in Figure 1b, the probability of the electron’s magnetic moment facing downwards and upwards will be equal because the total magnetic moment in the ocean of atoms is zero. This situation is that “the energy band does not undergo spin splitting”, meaning that when the electron is in the spin-up energy band, the energy of the system is equal to that when it is in the spin-down energy band (the energy band in the right figure of Figure 1b is gray, indicating that the energy of the electron with an up and down moment is strictly equal).
Due to the lack of macroscopic magnetism in antiferromagnets, the atomic magnetic moment is difficult to be controlled by external fields. For example, when the magnetic head (ferromagnet) approaches an antiferromagnetic tape, the atomic magnetic moment in the antiferromagnet will remain unchanged. This makes antiferromagnets difficult for information writing and reading like ferromagnetic storage media. For this reason, the discoverer of antiferromagnetic materials and Nobel laureate Louis Néel believes that antiferromagnetic materials are “interesting but useless”. However, in some aspects, antiferromagnets have undeniable advantages over ferromagnets. For example, the unique terahertz spin dynamics of antiferromagnets can achieve extremely fast, picosecond-scale magnetic moment reversal.
From the above analysis, it is not difficult to see that an ideal next-generation spintronic material needs to have the characteristics of ferromagnets that are friendly for information exchange, as well as the ability of antiferromagnets to store information with high stability and density, and ultrafast spin dynamics properties. This seems to be a contradictory requirement. However, a special type of antiferromagnet has recently been predicted through theory. Although they do not exhibit macroscopic magnetism, the spin of their energy bands split like the ferromagnets, which means they exhibit spin-polarized transport behavior.
Figure 1c is a simple schematic diagram of this novel material. In this magnet, the magnetic moments are arranged in the opposite direction like traditional antiferromagnets, and the total moment remains zero. But what’s important is that the shape of a spin-up small magnet is different from that of a spin-down small magnet: one is relatively “long”, and the other is relatively “flat”. In this way, the two sublattices with different spin directions cannot be connected through spatial translation or inversion operations (i.e., when the first small magnet is translated to the second, their shapes cannot match). Strictly speaking, the occurrence of this spin splitting phenomenon requires the system to simultaneously break PT and Uτ symmetries. Here, P and T refer to the spatial inversion and the time-reversal symmetry operators, respectively; U and τ refer to the spin-flip and the lattice translation operators, respectively.
Surprisingly, according to theoretical predictions, the spins of energy bands of such antiferromagnets split; the spin on the left half of a band is completely opposite to that on the right half (as shown in the right figure of Figure 1c). The “altermagnets” which has recently attracted widespread attention belongs to this type of unconventional antiferromagnet.
Phenomena such as the spin-polarized current, the anomalous Hall effect, the magneto-optical effect, etc., that were originally only observed in ferromagnets, were gradually realized in such unconventional antiferromagnets. That is to say, unconventional antiferromagnets can serve as generators and manipulators of spin currents, as well as functional layers to generate Majorana zero modes, spin pumping effects, and Josephson effects. Their emergence has broken the “useless” impression of antiferromagnetic materials and is expected to replace ferromagnets as the material foundation of spintronics.
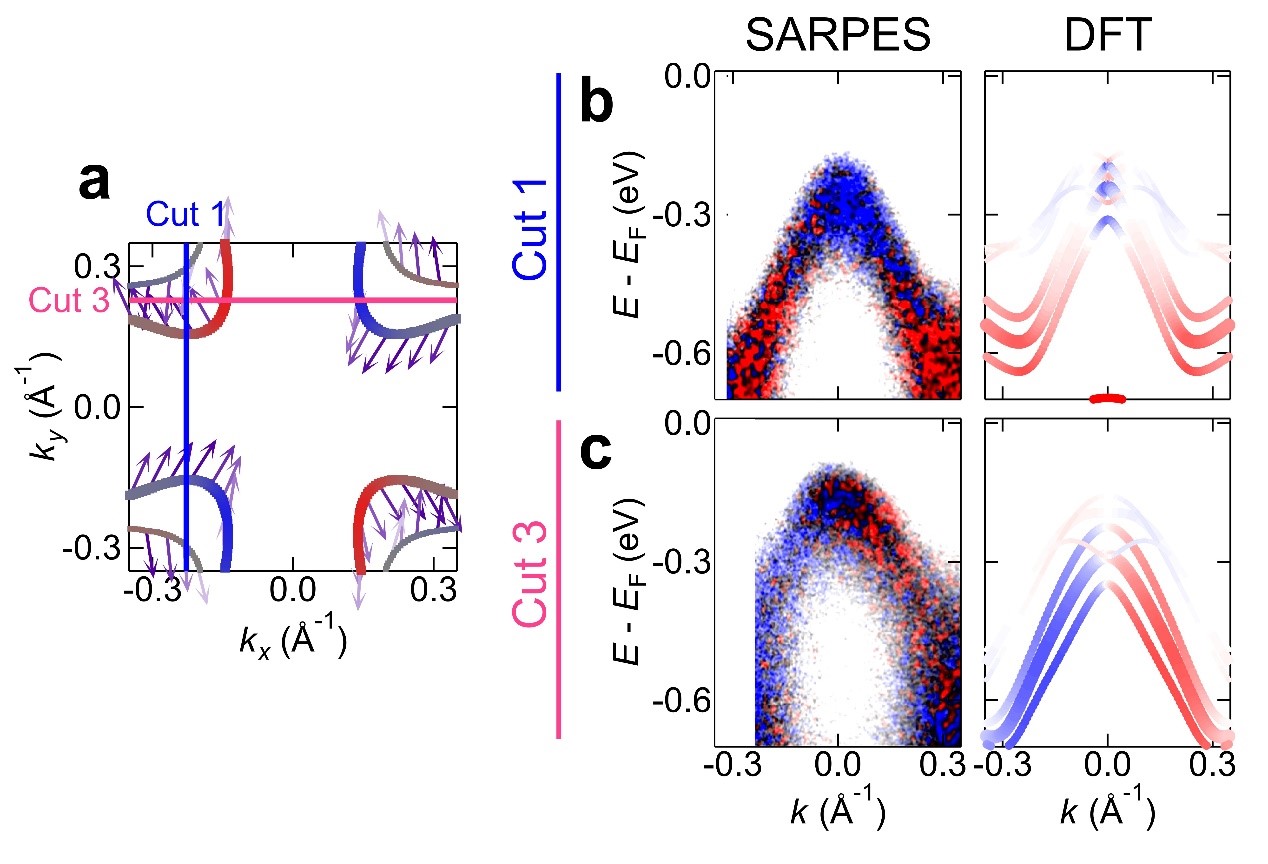
Figure 2. Electronic structure of MnTe2 using SARPES and DFT calculations. The blue and red colors in the figure represent two different spins. (a) Spin-resolved constant energy contour calculated by DFT. Spin Sα is defined along kα (α = x, y, z). (b & c) Spin-resolved energy bands along Cut 1 and Cut 3 were obtained by SARPES and DFT, respectively.
Theoretical research on unconventional antiferromagnets with spin splitting has flourished, and Prof. Qihang Liu’s group is at the forefront of the world in this field. However, experimental research on these magnets is still very scarce, especially with regard to their most important characteristic, the direct measurement of spin splitting energy bands, is still lacking. This measurement can undoubtedly prove the existence of spin splitting and has profound significance for the development of magnetic materials and spintronics. The best method for observing the spin splitting energy bands is the spin- and angle-resolved photoemission spectroscopy (SARPES). This advanced technique can directly and quantitatively measure the band structure and the spin of solids.
In this work, the research team conducted a detailed study on the band spin of antiferromagnet MnTe2, which meets the symmetry requirements for spin splitting, using SARPES and theoretical calculations. MnTe2 is a noncoplanar antiferromagnet with inversion symmetry, therefore, it is not an altermagnet. However, the mechanism of its spin splitting is exactly the same as that of an altermagnet. First-principles calculations based on density functional theory (DFT) indicate that its energy bands are highly spin polarized, and the spin polarization direction is antisymmetric with respect to the high symmetry planes of the Brillouin zone (the smallest repeating unit in the momentum space where the energy band is located). SARPES data in Figure 2 shows that the bands along Cut 1 and Cut 3 exhibit significant spin polarization along the x direction. There is opposite spin polarization at the top and both ends of the band along Cut 1, while the bands along Cut 3 exhibit antisymmetric spin polarizations with respect to the kx = 0 plane.
These results are consistent with the DFT calculations (Figure 2b,c). By changing the magnitude of the out-of-plane momentum, the research team found that the band spin is also antisymmetric with respect to the kz = 0 plane. In addition, when the temperature of the material rises above a specific temperature, the system becomes paramagnetic. SARPES measurements at elevated temperatures show that the spin polarization almost disappears. The data thus unquestionably demonstrates that MnTe2 exhibits the desired spin splitting induced by antiferromagnetism.
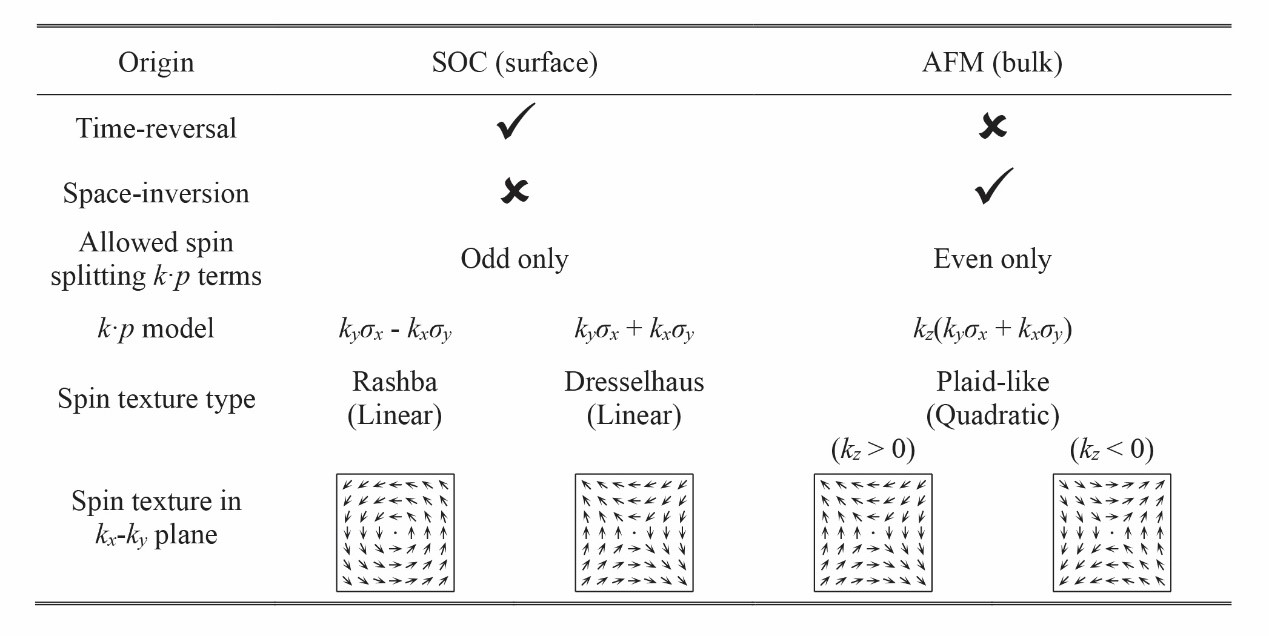
Table 1. Spin splitting in MnTe2 caused by surface spin-orbit coupling and by bulk antiferromagnetic order, including symmetry, k · p model, and allowed in-plane spin texture types.
The team further found significant differences in spin splitting caused by antiferromagnetic order in MnTe2 and that caused by spin-orbit coupling in traditional non-magnetic systems (such as Rashba- and Dresselhaus-types). For the latter, due to the existence of time-reversal symmetry, the system needs to break the spatial inversion symmetry. In that case, the k · p Hamiltonian only allows odd-order polynomials of momentum k, such as the linear Rashba or Dresselhaus terms. For antiferromagnetic MnTe2, the lattice has spatial inversion symmetry and breaks time-reversal symmetry, so only even-order spin splitting terms of momentum k are allowed. Thus, a novel quadratic spin texture is formed (Table 1).
This work discovers experimentally the unconventional antiferromagnet with spin splitting energy bands, which has guiding significance for future research and application of antiferromagnetic spintronics. During the research process, the researchers attempted various candidate materials and ultimately selected MnTe2 with larger antiferromagnetic domains. They also overcame technical difficulties, such as frequent instrument malfunctions.
Yu-Peng Zhu, a PhD student in Chang Liu’s group, and Xiaobing Chen, a postdoctoral fellow in Qihang Liu’s group, are the first authors of the paper. Chang Liu, Qihang Liu, and Shan Qiao are the co-corresponding authors. Collaborators of the paper include Prof. Rui-Hua He’s group from Westlake University, Dr. Yaobo Huang from BL09U (Dreamline) of the Shanghai Synchrotron Radiation Facility (SSRF), Prof. Jörg Wrachtrup’s group from the University of Stuttgart in Germany, Prof. Dawei Shen, Mao Ye, and Zhengtai Liu’s group from BL03U of SSRF, Masashi Arita from Hiroshima Synchrotron Radiation Light Source (HiSOR) in Japan, and Dr. Kiyohisa Tanaka from the UVSOR Light Source in Japan. The Department of Physics and SIQSE of SUSTech is the first affiliation of the paper.
This work was supported by the National Key R&D Program of China, National Natural Science Foundation of China (NSFC), Key-Area Research and Development Program of Guangdong Province, Guangdong Provincial Key Laboratory, Guangdong Innovative and Entrepreneurial Research Team Program, and the Shenzhen Science and Technology Program.
Paper link: